
The Paris Agreement set a long-term goal of limiting global warming to “well-below” 2C above pre-industrial levels and to pursue efforts to restrict it to 1.5C.
A key question for the upcoming rounds of the international climate negotiations, particularly when countries review their climate commitments next year, is exactly how fast would we have to cut emissions to reach these goals?
In a new paper, published in Nature Geoscience, we provide updated estimates of the remaining “carbon budget” for 1.5C. This is the total amount of CO2 emissions that we can still emit whilst limiting global average warming to 1.5C.
Our estimates suggest that we would have a remaining carbon budget equivalent to around 20 years at current emissions rates for a 2-in-3 chance of restricting end-of-century warming to below 1.5C.
This suggests that we have a little more breathing space than previously thought to achieve the 1.5C limit. However, although 1.5C is not yet a geophysical impossibility, it remains a very difficult policy challenge.
Earth system models and 1.5C
The single most important factor in the extent of future global warming is our cumulative emissions of CO2, which – due to the very long timescales of the natural carbon cycle – creates warming that persists for thousands of years.
This means scientists and policymakers focus on the total stock of CO2 that we put into the atmosphere, rather than the flow of CO2 in any particular year.
Our paper looks at different ways of estimating the total amount of CO2 we can emit into the atmosphere and still have a good chance of limiting temperature rise to 1.5C – known more simply as the 1.5C “carbon budget”.
Earth System Models (ESMs) – computer programmes that simulate the fundamental physics of the ocean, atmosphere and carbon cycle – can give us estimates of budgets for future emissions that might be compatible with 1.5C. They do this by counting emissions produced in the model between today and when the model’s warming reaches 1.5C.
However, in general, ESM projections don’t match exactly with how much warming we’ve seen – they display slightly more warming for slightly less cumulative CO2 than we’ve seen in the real world.
Taken on their own, these discrepancies are relatively modest and are unsurprising given the inherent challenges in constructing computer models of the entire Earth system. But they can substantially affect estimates of the remaining carbon budget for 1.5C.
The chart below shows projected warming (y-axis) from a collection of ESMs as cumulative CO2 emissions increase (x-axis). The coloured lines show emissions and warming according to four greenhouse gas scenarios known as “Representative Concentration Pathways”. These range from the low-end, where atmospheric CO2 concentration peaks and then falls during this century (RCP2.6), to the high-end, with no action to reduce global emissions (RCP8.5).
The black cross shows where we stand today: with 545bn tonnes of carbon emitted (as of the end of 2014) and human-caused warming of around 0.9-1C since pre-industrial times. This total of 545bn tonnes of carbon is equivalent to around 2,000bn tonnes of CO2.

Cumulative emissions since 1870 and warming relative to the period 1861–80. The red and grey plumes show the 5–95% range of model simulations under the different RCP scenarios and 1% annual CO2 increase scenarios, respectively. Thick coloured lines show the average model response to the RCP scenarios. Ellipses show cumulative emissions and warming in 2100 for different categories of future emissions scenario. Black cross shows 2015 human-induced warming and observed cumulative emissions. The dashed black horizontal line is at 1.5C warming above pre-industrial and the black vertical dashed line is placed at the the value of cumulative emissions from 1870 when one third of the Earth System Models have crossed 1.5C Source: Millar et al. (2017), adapted from the IPCC Synthesis Report.
Taking an average across ESMs suggests that our cumulative emissions to date would correspond to about 0.3C more than best estimates of human-caused warming so far.
If we zoom in specifically on the cross, we can see this difference more clearly. The red arrow shows the gap between current human-caused warming and what the ESMs projected.
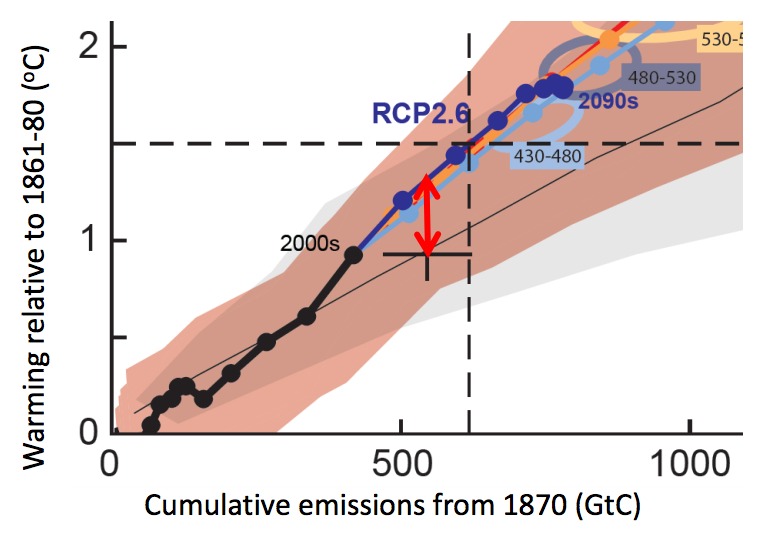
As earlier chart, but with red arrows to show difference between models and observed warming. Credit: Richard Millar (adapted from Figure 1 of Millar et al., 2017).
For a global temperature rise of 3C or 4C, this discrepancy would be relatively insignificant for the remaining carbon budget. However, for such an ambitious target as 1.5C, 0.3C can make a substantial difference when calculating how much remaining CO2 we can still emit without pushing us over 1.5C of warming when the remaining budget is calculated by simply subtracting off estimates of cumulative emissions to date from the ESM-based budgets for 1.5C relative to preindustrial (i.e. the horizontal difference between the cross and the vertical dashed black line in the figure above).
For example, analyses of remaining carbon budgets often use ESM-derived numbers from the Intergovernmental Panel on Climate Change’s (IPCC) most recent assessment report, and calculate remaining budgets using observed cumulative emissions to date. Such analyses suggest we now have less than four years of current emissions before the budget is spent.
Such small remaining budgets seem quite difficult to square with our understanding of the present state of the climate system and would require a substantial and rapid changes in the remarkably constant relationship between observed warming and observed cumulative emissions that we have seen so far.
Re-estimating the remaining carbon budget
In our paper, we ask a different question of these ESMs, namely what is the cumulative CO2 emissions budget, from today onwards, compatible with levels of simulated warming on top of the model’s present warming?
In other words, if human-caused warming over this decade was – on average – about 0.9C, a budget for 1.5C above preindustrial corresponds would correspond to a budget for 0.6C more human-caused warming from this decade on.
We investigated what ESMs can tell us about such budgets. This approach allows us to examine what the models say about future warming relative to future emissions, without bringing in any potential model bias simulated over the historical period.
This method gives an estimate for the remaining 0.6C of warming of about 880bn tonnes of CO2, from the beginning of 2015. This is about equal to about 20 years at current annual emissions, or alternatively, a straight line decrease in CO2 emissions from today’s values to zero in about 40 years. (In the paper, we also provide budgets for various different warming thresholds above the present decade to allow for uncertainty in present day human-created warming, and therefore, the remaining warming until we reach 1.5C.)
It’s worth noting that this budget explicitly considers a scenario that assumes strong action to reduce the contribution of non-CO2 gases (such as methane) to future warming is also undertaken alongside limiting CO2 emissions. This is a more plausible representation of a world with future climate policy than assuming a more business-as-usual scenario for these other pollutants – as has often been done when calculating budgets in the past.
Adaptive climate policy
Another approach we used to calculate carbon budgets is to mirror the regular “stocktakes” that will form part of the Paris Agreement. The aim of these stocktakes is to periodically ratchet up the ambition of national commitments to reducing CO2 and help ensure that a “well below 2C” world is actually achieved.
To model carbon budgets under such an adaptive process more directly, we use a simple climate model capable of taking into account the present climate state and important uncertainties such as exactly how strongly the climate will respond to CO2 emissions.
With this simple model, we construct pathways in which emissions are continually adapted over time in order to actually achieve a warming of 1.5C in 2100 no matter what the climate response turns out to be. This mimics an adaptive climate policy under the Paris Agreement’s pledge-and-review system – and assumes it’s successful.
Estimated in this way, we find the remaining carbon budget for a 66% probability of limiting warming to 1.5C in 2100 is 915bn tonnes of CO2 (from the start of 2015). This number is consistent with our ESM estimates given earlier, and again assumes very aggressive action to reduce non-CO2 contributions to warming.
Our results show that very aggressive future emissions reduction pathways, in which rapid and deep mitigation begins today (not 5-10 years earlier as in many emissions scenarios), would be approximately consistent with the long-term temperature goals of the Paris Agreement.
This suggests that achieving the goal of 1.5C warming is not yet a geophysical impossibility.
Policy implications for the Paris process
Even if it is still geophysically possible to limit warming to 1.5C, a more important question is whether it is economically, socially and politically feasible?
Due to the still very tight carbon budgets, achieving the 1.5C goal will require global CO2 emissions to be at or below zero in the second half of this century. Achieving 1.5C may, therefore, require substantial deployment of negative emissions technologies, which at the moment remain untested at large scales.
Emissions scenarios compatible with 1.5C could also require very high maximum rates of decarbonisation, comparable only with those seen for past emissions during short periods of recession or war.
You can see this in the chart below, which shows an idealised scenario of falling emissions (dashed line). This assumes global emissions peak in the next year or two and then decline in a straight line, achieving net zero emissions shortly after mid-century, corresponding to a 66% probability of less than 1.5C of warming in 2100 (narrow orange line).

Idealised mitigation trajectories meeting the 1.5C target. We construct an idealised future emissions pathway (dashed; left hand axis) that declines linearly from 2020 to zero in 2055, with cumulative emissions since the start of 2015 ~880bn tonnes of CO2. The solid orange lines (right hand axes) shows the 50th percentile (thick) and 66th percentile (thin) of the climate responses to this emissions scenario when coupled with aggressive reductions in non-CO2 contributions to warming. The 66th percentile line falls just below 1.5C in 2100. Coloured shading shows different percentile ranges of the climate projection for global mean warming. Credit: Richard Millar (adapted from Figure 3 of Millar et al., 2017).
A key challenge for climate policy is, therefore, to find ways to sustain high decarbonisation rates for decades at a time in an economically feasible way.
Enhancing near-term emissions reduction ambition could help address some of these feasibility challenges. Even 1.5C-compatible scenarios with the most limited near-term ambition (and, hence, the most rapid decarbonisation later on) require larger cuts in carbon emissions than initially pledged under the Paris Agreement for 2030.
The fact that 1.5C may still just about be geophysically possible, therefore, certainly doesn’t mean that climate policy has any time to relax. If anything, it provides an important incentive to work to enhance the Paris pledges further, at the first opportunity, if governments are serious about the 1.5C ambition.
Estimates of the remaining carbon budget for 1.5C will inevitably be sensitive to the estimated value of present day human-induced warming, and will be more so as the limit approaches. Careful and up-to-date monitoring of present and projected human-induced warming will be essential to the Paris process as it tackles the challenge of limiting warming to 1.5C – as will a good dialogue between scientists and decision-makers to ensure that the latest knowledge about the climate system is effectively communicated to policymakers.
Our results indicate that based on the current understanding of the Earth system, the window for achieving 1.5C is still narrowly open. If very aggressive mitigation scenarios can be implemented from today onwards, they may be sufficient to achieve the goals of the Paris Agreement.
Dr Richard Millar is a postdoctoral research fellow at the Oxford Martin Net Zero Carbon Investment Initiative.
This opinion piece originally appeared as a guest blog on Carbon Brief on 18 September 2017.
This opinion piece reflects the views of the author, and does not necessarily reflect the position of the Oxford Martin School or the University of Oxford. Any errors or omissions are those of the author.
